GeoGebra, a software system for dynamic geometry and algebra in the plane, since its inception in 2001, has gone from a dynamic geometry software (DGS), to a powerful computational tool in several areas of mathematics. Powerful algebraic capabilities have joined GeoGebra, an efficient spreadsheet that can deal with many kinds of objects, an algebraic and symbolic calculation system and several graphical views that expand the possibility of multidimensional representations. The recent 3D features allow more intuitive interaction with three-dimensional objects. However, there are still many open questions in GeoGebra’s 3D capabilities, namely at the intersection of two surfaces.

In this presentation will be shown a representation method of the intersection of two quadric as well as obtaining some it’s algebric information, using resultants, subresultants and the Sturm–Habicht sequence.

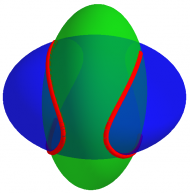
Also, in this communication will be presented some constraints of developed work and presented, in a summary way, some of the goals for future work.

References
[1] Gonzalez-Vega, L. (1997). Implicitization of Parametric Curves and Surfaces
by using Multidimensional Newton Formulae. Journal of Symbolic Computation, 23(2–3), 137–151. http://doi.org/10.1006/jsco.1996.0080
[2] Fioravanti, M., Gonzalez-Vega, L., & Necula, I. (2006). Computing the intersection of two ruled surfaces by using a new algebraic approach. Journal of Symbolic Computation, 41(11), 1187–1205. http://doi.org/10.1016/j.jsc.2005.02.008
[3] Li, Y.-B. (2006). A new approach for constructing subresultants. Applied Mathematics and Computation, 183(1), 471–476. http://doi.org/https://doi.org/10.1016/j.amc.2006.05.120