Título: Quod Erat Demonstrandum [qed/cqd]

Responsáveis:Vítor Hugo Fernandes e Manuel Messias (Departamento de Matemática da FCT/UNL)

Monitor:  Andreia Bártolo (Licenciatura em Matemática na FCT/UNL)

Sala:  Sala 1.3 do Edifício VII

Resumo:Este curso destina-se a todos os alunos do Ensino Secundário que não tenham olhos verdes ou tenham nariz aquilino, mas sejam raparigas ou não tenham cabelo ruivo, a não ser que sejam rapazes ou tenham olhos verdes, mas tenham cabelo ruivo ou não tenham nariz aquilino. Estás confuso(a)? Então vem aprender a sistematizar o raciocínio! Iremos estudar lógica elementar e aprender estratégias para fazer demonstrações matemáticas simples (e complexas!)...

Título: Sabes qual é a probabilidade de ganhares o euromilhões?

Responsáveis:Ayana Mateus e Inês Sequeira (Departamento de Matemática da FCT/UNL)

Monitor:  Tiago Nunes (Licenciatura em Matemática na FCT/UNL)

Sala: Sala 1.4 e Laboratório 2.5 do Edifício VII

Resumo:A incerteza é algo que afeta com maior ou menor profundidade toda a nossa atividade quotidiana, abrangendo todos os ramos do saber. O que vos propomos aqui, é a tentativa de quantificar alguns dos acontecimentos com que somos confrontados na nossa vida, através do cálculo de probabilidades. De forma a facilitar esse cálculo, faremos uma breve incursão pelo mundo da análise combinatória. Partindo de um conjunto com um número finito de elementos, como por exemplo, números, pessoas, objetos, letras, etc, formar-se-ão sequências ou subconjuntos possíveis. E por fim, calcularemos a probabilidade de ganhar o euromilhões!

Título: Matemática Computacional

Responsáveis:Nuno Martins e Magda Rebelo (Departamento de Matemática da FCT/UNL)

Monitor: Diogo Cosme  (Licenciatura em Matemática na FCT/UNL)

Sala: Laboratório 2.6 do Edifício VII

Resumo: Genericamente, pode dizer-se que a matemática computacional é um ramo da matemática que procura desenvolver métodos matemáticos (bem condicionados) e algoritmos computacionais (estáveis) para resolver problemas. Por exemplo, desde problemas de reconstrução/tratamento de imagens (com aplicações em áreas como medicina e computação gráfica) até problemas de construção de superfícies tridimensionais (úteis no desenvolvimento de filmes de animação), são muitos os exemplos de problemas cuja resolução é obtida computacionalmente. Em geral, a resolução computacional destes problemas é obtida por intermédio de aproximações numéricas. Isto porque, ora a solução analítica não é conhecida ou então o seu cálculo poderá envolver um elevado esforço computacional. Neste curso abordaremos a construção e análise computacional de métodos matemáticos para a resolução de alguns problemas clássicos.

Ver imagem

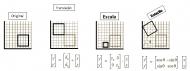
Título: Matrizes no dia-a-dia

Responsáveis:Ana Cristina Casimiro e João Cabral (Departamento de Matemática da FCT/UNL)

Monitor:  Duarte Chambel  (Licenciatura em Matemática na FCT/UNL)

Sala: Sala 1.5 do Edifício VII

Resumo:  Vamos ver como uma ideia tão simples como uma matriz (tabela rectangular) cujas entradas são números ou outros símbolos nos pode ajudar a resolver problemas do nosso quotidiano. Entre outras aplicações que podemos explorar estão a computação gráfica, os modelos económicos, os circuitos eléctricos, a organização de uma floresta ou até jogos de estratégia.