Curso/Projecto 1

Título: Matemática Financeira

Responsáveis: Marta Faias e Pedro Mota 

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Tiago Cordeiro

Resumo: Diariamente são transacionados milhares de milhões de euros em ativos financeiros por todo o mundo. Quer sejam ações de empresas, quer sejam produtos financeiros complexos, a matemática é fundamental para perceber as dinâmicas que estão por trás dos seus preços. Neste projeto pretende-se que os alunos aprendam a determinar e reproduzir os preços de alguns desses ativos utilizando o conceito de não arbitragem e a famosa fórmula de Black-Scholes.

Curso/Projecto 2

Título: Equações diferenciais - uma introdução

Responsável: José Maria Gomes

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Vítor Augusto

Resumo: Uma equação diferencial é uma equação cuja incógnita é uma função, relacionando os valores da função com os da sua derivada. Por exemplo, a função exponencial é solução da equação diferencial y'=y. As equações diferenciais são um ramo muito importante da Matemática. Elas permitem modelar e resolver problemas em áreas tão diversas como a física, a economia ou a biologia. Neste pequeno curso da MatNova começaremos por aprender a resolver equações diferenciais muito simples. Depois iremos aplicar os nossos conhecimentos em dois problemas célebres de datação cuja resolução pôs um termo a debates acesos sobre a autenticidade de pinturas: a saber, as pinturas rupestres de Altamira e o quadro 'A ceia em Emaus' que nos anos trinta foi atribuído a Vermeer. Finalmente -se tivermos tempo- veremos como a resolução de uma equação diferencial nos permite construir um forno solar.

Curso/Projecto 3

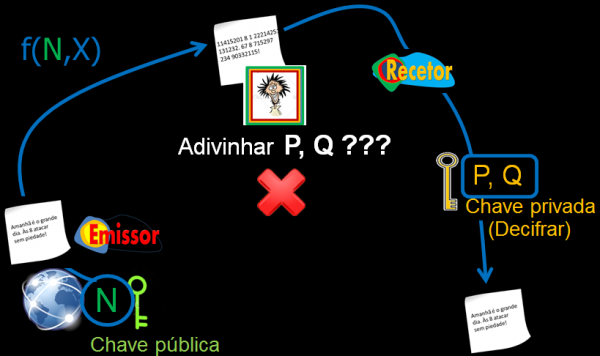
Título: M4t3m4t1c4, 35p1õ3% e R41nh4% D3c4p1t4d4%

Responsáveis: Cláudio Fernandes e Joaquim Nogueira  

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Filipe Lopes

Resumo: Conseguiste decifrar o nome do Curso? Então estás apto a realizá-lo connosco. Vamos viajar juntos pela História da Criptografia e descobrir como o seu desenvolvimento foi fundamental no desfecho drástico de guerras, monarquias e vidas individuais. Nessa viagem vais aprender alguns dos principais Métodos e Algoritmos de Criptografia e a Matemática envolvida em cada um deles. Ficarás a saber a importância dos números primos nos processos de codificação modernos e no final terás aprendido muita Matemática, conseguirás fazer contas secretas e, com o resto do grupo, vais conseguir comunicar com um código e um programa só nosso!  4t3´ j4´!

Curso/Projecto 4

Título: Para o transfinito e mais além...

Responsáveis: Fátima Rodrigues e Manuel Messias

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Tânia Paulista

Resumo: Sabias que na Matemática há infinitos com “tamanhos” diferentes? Poderíamos assim dizer que há infinitos mais infinitos que outros!? A teoria dos números transfinitos remonta a 1872 e é sobretudo uma criação do notável matemático russo Georg Cantor (1845-1918) um dos principais fundadores da Teoria dos Conjuntos. Neste breve curso pretendemos abordar os conceitos básicos da teoria dos conjuntos com especial ênfase na noção de cardinal infinito.

Curso/Projecto 5

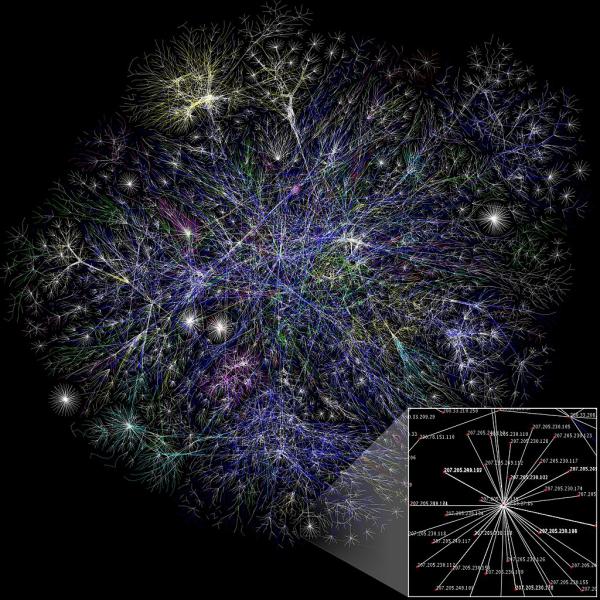
Título: Vivemos num Mundo de Redes

Responsáveis: João Cabral e Isabel Cabral 

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Ana Marques

Resumo: As redes permitem analisar as interacções, muitas vezes complexas, presentes em diversos sistemas sociais, físicos e tecnológicos. Da Internet à ecologia, da medicina aos sistemas financeiros tudo pode ser melhor compreendido recorrendo a redes. Neste curso apresentamos alguns conceitos básicos desta teoria bem como alguns algoritmos.

Curso/Projecto 6

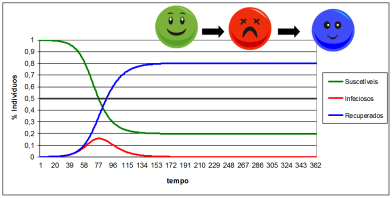
Título: A matemática das epidemias e vacinas

Responsáveis: Paula Patrício e Magda Rebelo

(Departamento de Matemática, FCT NOVA, UNL)

Monitor: Rita Caneco

Resumo: Desde o início da vacinação em massa a prevalência de sarampo diminuiu drasticamente e, em muitos países, o sarampo considera-se eliminado. No entanto, recentemente surgiram diversos surtos, como o caso da Disneylândia, nos Estados Unidos, no final de 2014 e mais recentemente em alguns países da Europa, incluindo Portugal. O que será necessário para controlar uma doença por vacinação? Porque aparecem estes surtos?
Neste curso vamos aprender como a matemática nos pode ajudar a compreender este problema. Aproveitamos para conhecer várias áreas da matemática que estão envolvidas no estudo dos modelos matemáticos para o estudo da transmissão de doenças, desde as equações diferenciais até à análise numérica.