CURSO/PROJETO 1

Título: Matemática Financeira

Docentes: Pedro Mota e Marta Faias

Monitor:

Resumo: Diariamente são transacionados milhares de milhões de euros em ativos financeiros por todo o mundo. Quer sejam ações de empresas, quer sejam produtos financeiros complexos, a matemática é fundamental para perceber as dinâmicas que estão por trás dos seus preços. Neste projeto pretende-se que os alunos aprendam a determinar e reproduzir os preços de alguns desses ativos utilizando o conceito de não arbitragem e a famosa fórmula de Black-Scholes. Mesmo conhecendo a dinâmica dos preços dos ativos financeiros, as transações nos mercados financeiros  envolvem sempre risco. Neste projeto os alunos irão também aprender quais são esses riscos e irão implementar alguns dos métodos da matemática que os permitem minimizar.

CURSO/PROJETO 2

Título: Conjuntos, boas ordens e ordinais: a definição dos naturais.

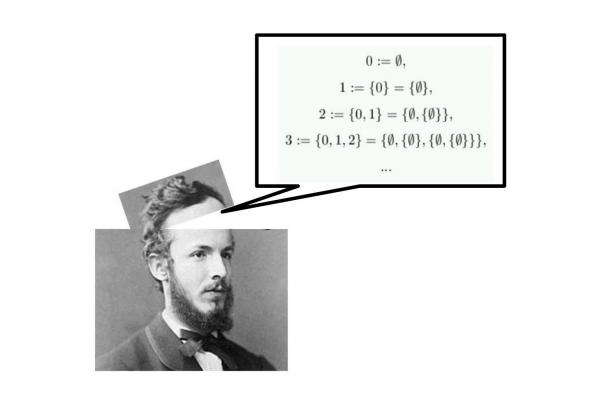
Docentes: Jorge André e Manuel Messias

Monitor:

Resumo: Os ordinais foram apresentados por Georg Cantor (1845-1918) em 1883 para classificar conjuntos com certos tipos de estruturas de ordem neles sendo, sobretudo, uma criação desse notável matemático russo, um dos principais fundadores da Teoria dos Conjuntos. Neste breve curso pretendemos abordar os conceitos básicos da teoria dos conjuntos com especial ênfase na noção de ordinal e na definição dos naturais como ordinais finitos.

CURSO/PROJETO 3

Título: Estatística: perceber o mundo através dos dados.

Docentes:  Isabel Natário e Dora Gomes

Monitor:

Resumo: A tecnologia tem facilitado e promovido a recolha sistemática e global de dados, como ficou bem patente neste último ano pandémico. A estatística foca-se na organização e interpretação destes dados, extraindo mais e melhor informação e transformando-a em conhecimento útil, efetivamente usando os dados para melhor compreender o mundo que nos rodeia! 

Este curso aborda aspetos de formação base em Estatística Descritiva para a obtenção de tal entendimento. Cobre técnicas de exploração, visualização, resumo e análise de dados, no contexto de exemplos reais, analisados na prática com a ajuda de um software estatístico apropriado para as análises.

CURSO/PROJETO 4

Título: Epidemias, modelar e simular para compreender!

Docentes: Alice Castelhano, Magda Rebelo e Paula Patrício

Monitor:

Resumo: A pandemia que vivemos veio nos mostrar como os modelos matemáticos são úteis para descrever a propagação de doenças contagiosas. Neste curso vamos ver como funcionam! Vamos construir o nosso próprio modelo matemático e explorar como incluir fenómenos importantes no decurso de uma epidemia como as medidas de controlo, a vacinação e/ou o comportamento humano.

CURSO/PROJETO 5

Título: Curvas de perseguição

Docentes: Luís Trabucho e alunos do Núcleo de Matemática

Monitor:

Resumo: Se E for um evasor com velocidade u e P for um perseguidor com velocidade v > u, então P poderá apanhar E (independentemente do que E possa fazer): bastará ir até à posição inicial de E e seguir o caminho por este traçado. A trajectória descrita por P designa-se por curva de perseguição. Mas poderá haver uma outra trajectória a que corresponda um menor tempo e/ou uma menor distância. Estas situações poderão ser: uma criança (P) a tentar apanhar outra (E); um navio pirata (P) a tentar abordar um galeão (E); um torpedo (P) a tentar atingir um navio (E); um predador (P) (raposa) a tentar caçar uma presa (E) (pequeno animal); Aquiles (P) a tentar apanhar uma tartaruga (E); o Minotauro (P) a tentar apanhar um jovem cidadão de Atenas (E); etc.

Neste projecto tentaremos compreender como é que a Matemática nos poderá ajudar a calcular curvas de perseguição, para uma grande variedade de problemas. Além disso, teremos oportunidade de admirar a enorme beleza deste tipo de curvas.

Conceitos básicos: Funções reais de variável real: máximos, mínimos, derivadas, representação gráfica. Funções trigonométricas.

CURSO/PROJETO 6

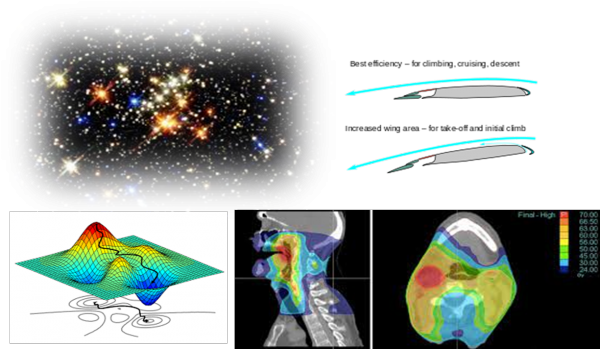
Título: O que têm em comum estrelas, asas de avião e radioterapia?

Docentes: Ana Luísa Custódio e Carmo Brás

Monitor:

Resumo: Como se calcula a idade de uma estrela? Como se projeta a geometria da asa de um avião? Como se planeiam as direções dos feixes de radiação em radioterapia? Neste projeto vais perceber a importância da Matemática na resolução destes e de muitos outros problemas, onde a palavra-chave é Otimizar. Recordando ou travando conhecimento com as derivadas, conceito muito útil em Otimização, iremos também abordar situações em que as derivadas não podem ser utilizadas, sendo necessárias alternativas ao seu uso. O projeto terá ainda uma componente computacional relacionada com a implementação de algoritmos numéricos de Otimização (não requer conhecimentos prévios de computação).